Quadratic Knapsack Problem

Problem Overview

The quadratic knapsack problem is one of the most popular variants of the single knapsack problem, with applications in many optimization contexts.

The aim is to maximize the value of individual items placed in the knapsack while satisfying a weight constraint. However, pairs of items also have positive interaction values, contributing to the total value within the knapsack.

Challenge Overview

For our challenge, we use a version of the quadratic knapsack problem. The size of the challenge instance is determined by the parameter $num\_items$, which is the number of items from which you need to select a subset to put in the knapsack.

The weight $w_i$ of each of the $num\_items$ is an integer, chosen independently, uniformly at random, and such that each of the item weights $1 \leq w_i \leq 50$, for $i=1,2,...,num\_items$. The values of the items are nonzero with a density of 25%, meaning they have a 25% probability of being nonzero. The nonzero individual values of the item, $v_i$, and the nonzero interaction values of pairs of items, $V_{ij}$, are selected at random from the range $[1,100]$.

The total value of a knapsack is determined by summing up the individual values of items in the knapsack, as well as the interaction values of every pair of items $(i,j)$, where $i > j$, in the knapsack:

We impose a weight constraint $W(S_{knapsack}) \leq 0.5 \cdot W(S_{all})$, where the knapsack can hold at most half the total weight of all items.

The quality of a solution is determined by how much better it is than a baseline value. The baseline value is determined by using a baseline algorithm. In particular a solution is given a quality score $better\_than\_baseline$ defined as $better\_than\_baseline = 1000*(V_{knapsack}-V_{baseline}) / V_{baseline}$. For precision, `better_than_baseline` is stored as an integer where each unit represents 0.01%. For example, a $better\_than\_baseline$ value of 150 corresponds to 150/10000 = 1.5% improvement over the baseline value.

Example

Consider an example of a challenge instance with $num\_items=4$. Let the baseline value be 46:

weights = [39, 29, 15, 43]
individual_values = [0, 14, 0, 75]
interaction_values = [ 0,  0,  0,  0
                       0,  0, 32,  0
                       0, 32,  0,  0
                       0,  0,  0,  0]
max_weight = 63

The objective is to find a high value set of items where the total weight is at most 63. Now consider the following selection:

selected_items = [2, 3]

When evaluating this selection, we can confirm that the total weight is less than 63, and the total value is 75,

Applications

The Knapsack problems have a wide variety of practical applications. The use of knapsack in integer programming led to breakthroughs in several disciplines, including energy management and cellular network frequency planning.

Although originally studied in the context of logistics, Knapsack problems appear regularly in diverse areas of science and technology. For example, in gene expression data, there are usually thousands of genes, but only a subset of them are informative for a specific problem. The Knapsack Problem can be used to select a subset of genes (items) that maximizes the total information (value) without exceeding the limit of the number of genes that can be included in the analysis (weight limit).

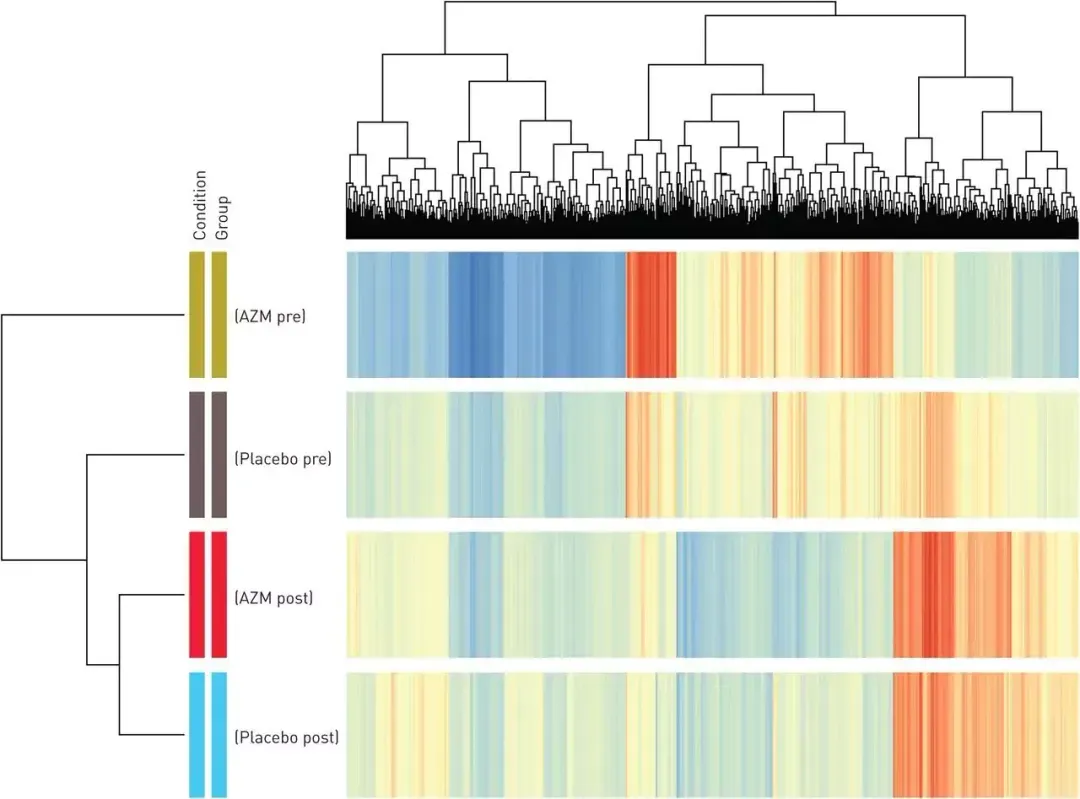
Figure 1: Microarray clustering of differentially expressed genes in blood. Genes are clustered in rows, with red indicating high expression, yellow intermediate expression and blue low expression. The Knapsack problem is used to analyse gene expression clustering.